Introducing Group Theory
I was talking with my partner's family recently and the topic of what particular courses she and I might be teaching wandered into the question of "what is modern algebra?" Since I am ostensibly a group theorist, I had to give the standard, glib response that (group theory at least) is the study and mathematical formalization of symmetry, which is a perfectly reasonable answer that doesn't really serve to give any particular understanding to someone who does not already know some group theory. More was said to explain, but I feel I really ought to write down something more substantial, so this article is exactly that!
My general aim is that the majority of this article be accessible to anyone willing to put a little bit of effort into understanding and doing the math in it, without requiring any special background. I'd recommend a paper, pencil, and a pair of scissors to follow along and to actually "do the exercises," so to speak. My group presentation visualizer is also a useful resource to have open in another tab; if you trust that the visualizer does what it says, it'll probably save you some work! Finally, some parts of this article have been rattling around since a linear algebra class I taught a while back and so I must, I'm afraid, actually include some numbers. It won't get any scarier than linear equations like \[ \begin{cases} 2x+3y=4\\ 5x-6y=7 \end{cases} \] and if you don't know or remember how to solve something like that, that's fine: I'll be giving the result anyway.
Symmetries of a Triangle
To start, what are the symmetries of a triangle? Maybe more precisely, imagine you cut an equilaterial triangle out of a piece of paper. How many ways can you place that paper cutout back into the hole you made? Try actually doing it and just count them out! It can help to label the front and back of the paper, as well as each side or each corner of the triangle. Three arrangements are shown below, with the different vertices of the triangle colored to help distinguish them.
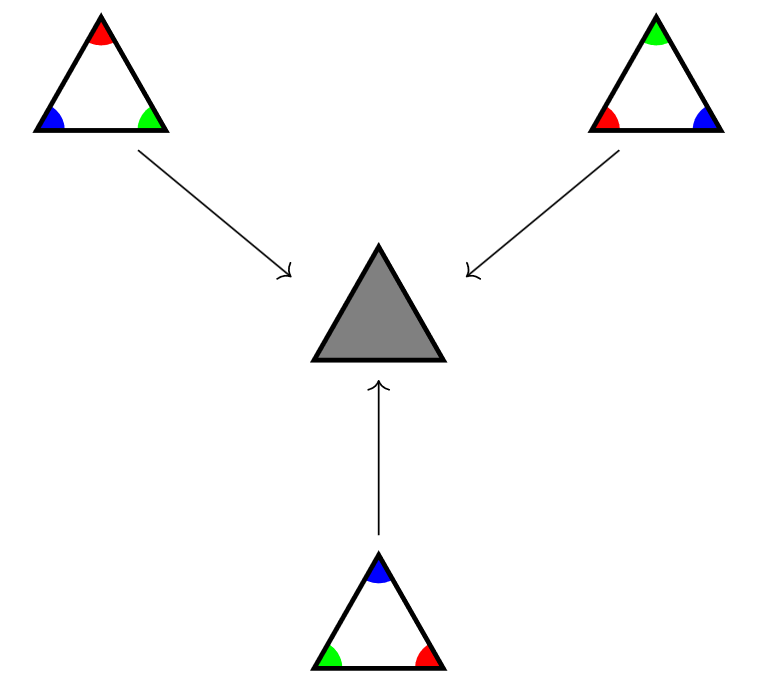
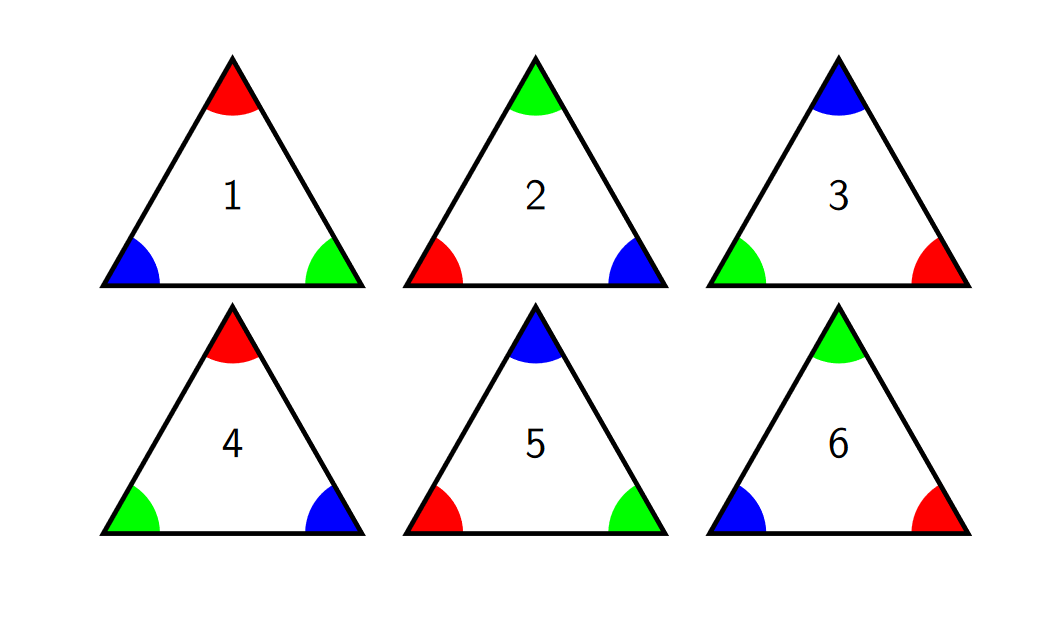
Playing around a little further, you should see that there are six arrangements total: three from rotating the triangle and then another three from flipping the triangle to its other side and rotating. (For those of you who know a little bit of group theory already, this is an application of the Orbit-stabilizer Theorem.) All six are shown below, with the rows being the front and back of the paper (more apparent if you labeled the paper or used two-colored origami paper). That is, the top row is the front of the paper facing up, in three rotations, while the second row is the back of the paper facing up, in three rotations.
Now, having counted up the six possibilities, we could dust off our hands and say we're done, but that's a bit unsatisfying. Moreover, just having counted up that there are six ways to replace our triangular cutout doesn't sufficiently capture the picture. The symmetries aren't just a list of six things, the symmetries are the ways in which we can move between those six positions. Take rotations for example. You can rotate either clockwise or counterclockwise. Here are the clockwise rotations:
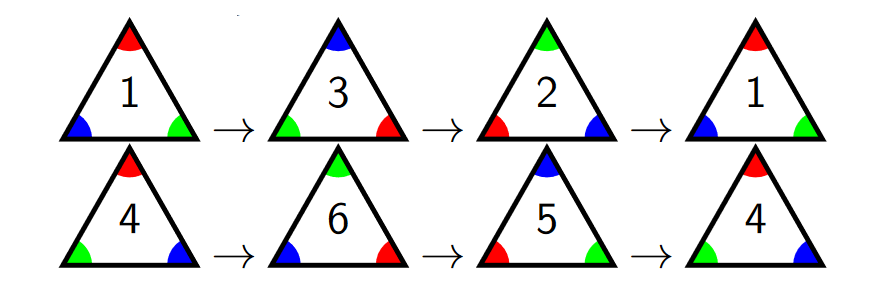
And here are the counterclockwise:
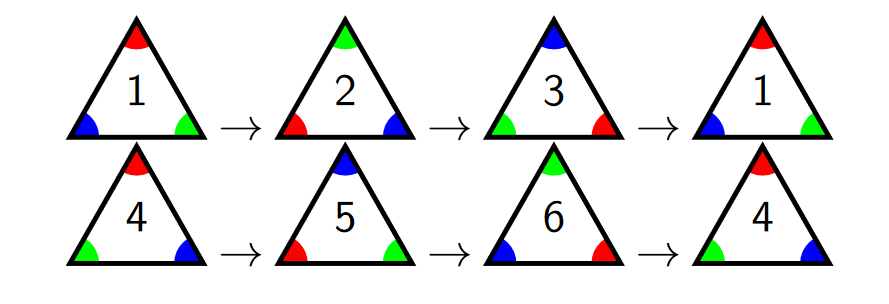
Likewise, we could choose an axis of a symmetry to reflect across. Here are reflections across a vertical axis and a diagonal axis:
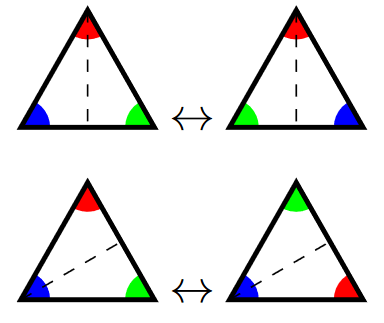
We could go on listing different motions for ages: there are other axes we could reflect across, we could combine rotation and reflection, and so on, but that gets pretty redundant. There are only six possible positions, so different motions do the same thing. Anywhere you can land by rotating counterclockwise, you can land by rotating clockwise, for example. This'll be our next specific goal: we want some sort of briefer notation or expression for our symmetries when we think of them as transforming from one of the six positions we found to another.
To that end, we're going to restrict to the following two motions:
- Rotating one-third of a revolution counterclockwise. We'll denote that by \(r\).
- Flipping across a vertical line of symmetry. We'll denote that by \(f\).
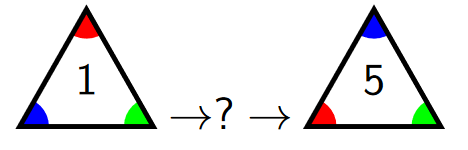 Here's one way to do it: \(rrf\).
Here's one way to do it: \(rrf\).
 And here's another: \(fr\).
And here's another: \(fr\).
 In any case, using our restricted list of motions \(r\) and \(f\), and being able to deduce what each of those motions does to any particular position on our triangular cutout, we can produce a nice, pictorial representation of the symmetries, as well as what position each motion sends us to:
In any case, using our restricted list of motions \(r\) and \(f\), and being able to deduce what each of those motions does to any particular position on our triangular cutout, we can produce a nice, pictorial representation of the symmetries, as well as what position each motion sends us to:
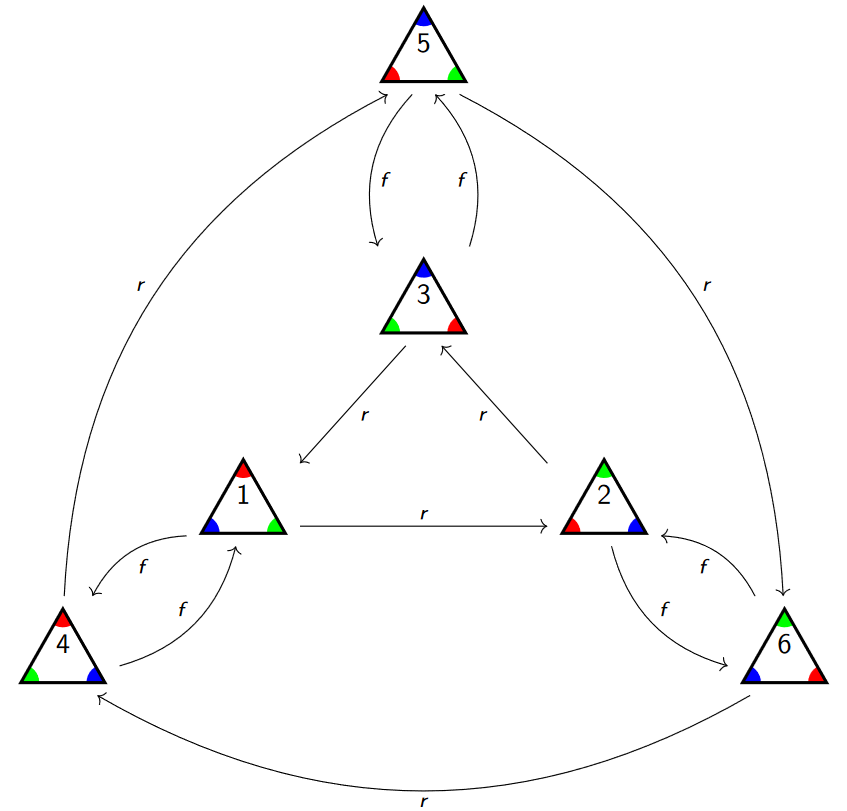 For those of you with some group theory background, you might recognize this as the Cayley Graph. Using this graph, we can describe any sequence of our symmetries \(r\) and \(f\) by following the appropriately labeled arrows. Indeed, we can visually check that we can transform from triangle 1 to triangle 5 by both \(rrf\) and \(fr\) by simply following the arrows from triangle 1 to triangle 5. We can find new ways, as well! It's quick to check that the path \(rfr\) also works.
For those of you with some group theory background, you might recognize this as the Cayley Graph. Using this graph, we can describe any sequence of our symmetries \(r\) and \(f\) by following the appropriately labeled arrows. Indeed, we can visually check that we can transform from triangle 1 to triangle 5 by both \(rrf\) and \(fr\) by simply following the arrows from triangle 1 to triangle 5. We can find new ways, as well! It's quick to check that the path \(rfr\) also works.
Presentations of Groups and an Algebraic Representation of our Symmetries
Thus far, we have stayed very geometric as we describe the symmetries of a triangle, which is pretty reasonable. We're working with a geometric object, after all. This results in a very visual interpretation that doesn't necessarily lend itself well to computation. To that end, we're going to introduce an algebraic system for describing symmetries: a presentation of a group. You don't need to know what a group is for this; for our purposes, we're going to treat the presentation as just a word game.
A presentation will consist of two parts: a list \(X\) of generators and a list \(R\) of relators, written \(\langle X:R\rangle\). The list \(X\) consists of some number of symbols (possibly infinitely many), usually just lower case letters like \(X=\{a, b, c\}\), say, just like what we were using to represent flips and rotations on the triangle. Using our generators \(X\), a word consists of some sequence of the letters from \(X\) or a second set of symbols \(X^{-1}\), the inverse of \(X\). That is, if \(X=\{a, b, c\}\), a word might be something like \(aba^{-1}cbc^{-1}\). You can think of each generator as some sort of symmetry, each inverse as the "opposite" of the symmetry (think clockwise and counterclockwise rotation), and each word as a sequence of symmetries to apply, just like the triangle example. The relators \(R\) consist of some list of words; we'll come back to the purpose of the relators in just a moment.
We need to hone in a little more on how we're treating words in our generators. Say I have the words \(ab^{-1}c\) and \(ca\). Generally, we want to think of these as some sequence of symmetries applied in order. That means we could apply both of these sequences, which we do by concatenating: \((ab^{-1}c)(ca)=ab^{-1}cca\) or \((ca)(ab^{-1}c)=caab^{-1}c\). Note that the order in which we concatenate does matter. Go back and convince yourself on the triangle example that \(rf\) and \(fr\) are different!
We generally call the concatenation multiplication, by analogy with notation like \((2)(3)=6\). We generally also extend those notation to write words a little more cleanly: rather than \(ab^{-1}cca\) we would write \(ab^{-1}c^{2}a\) as though we "multiplied" a variable \(c\) by itself, using exponent notation. Consequently, we need to deal with expressions like \(aa^{-1}\). Multiplicatively, this simplifies as \(aa^{-1}=1\). This is actually good for our notion of a word: we have an identity word! We want to treat "don't do anything" as a form of symmetry and so certainly \(aa^{-1}\) (think rotate clockwise, then counterclockwise) puts us back to where we started. Now, as far as words go, we allow for the "empty word," that is, we just don't write anything! As far as symmetry goes, that'd be our "do nothing" symmetry, so we generally write 1 as the empty word, for the sake of, well, being able to express the empty word. (As an aside, words are something written additively so \(ab^{-1}cca\) would be \(a-b+c+c+a\) and \(aa^{-1}=1\) as \(a-a=0\), swapping the multiplicative identity 1 for the additive identity 0, but we'll generally avoid this, since order matters a little more obviously with concatenation.)
Okay, now we can backtrack to what purpose the relators serve. As mentioned, the relators are a list of words in our generators. Their purpose is to tell us an additional list of rules for symmetries that "do nothing." This is a little easier demonstrated than explained. Say we have the presentation \(\langle a:a^{3}\rangle\). This consists of a single generator, \(a\), and a single relator, \(a^{3}\) (which is just \(a\) repeated three times). Our words consist of some number of \(a\) and \(a^{-1}\) in a row, like \(aa^{-1}a^{-1}a^{-1}\) or \(aaaa\). Using our multiplicative notation, we could simplify these, respectively, to \(a^{-2}\) and \(a^{4}\) (this is really just counting the total number of pluses and minuses). The relator \(a^{3}\) tells us the word \(a^{3}\) is trivial, that is, we can treat it like the empty word 1. This means, for example, we can "multiply by 1" (do nothing) by multiplying by \(a^{3}\) or, since it's the empty word, just delete \(a^{3}\) when it shows up. Take \(a^{-2}\) for example. Since \(a^{3}\) is trivial, nothing should change if I write \(a^{-2}\) as \(a^{-2}a^{3}\), which simplifying our multiplicative notation, is \(a\)! We've conclude that \(a^{-2}=a\). Similarly, \(a^{4}=a^{3}a=a\). We open ourselves up to all sorts of algebraic manipulation, using the rules given by the relators.
One brief comment before we hop back to interpreting our word game in terms of symmetries: we can be a little more flexible with how we write our relators. Let's say I gave you the presentation \(\langle a, b:aba^{-1}b^{-1}\rangle\). We have two generators and one relator, which is fairly simple as far as presentations go, but the algebraic manipulations possible from \(aba^{-1}b^{-1}\) being trivial aren't super obvious. It can often by nice to write the relator \(aba^{-1}b^{-1}\) as \(aba^{-1}b^{-1}=1\), so we can think a little more in terms of algebraic equations. There, we can balance equations, that is, perform the same operations on both sides of the equation and conclude useful algebraic information. For example, given \(aba^{-1}b^{-1}=1\) we can right multiply by \(ba\) (being very careful with the order, since order matters!) to get \(aba^{-1}b^{-1}ba=ba\). Cancellation between inverses simplifies this to \(ab=ba\). We could, if we like, write the presentation as \(\langle a, b:ab=ba\rangle\) which tells us immediately a very nice fact: the order of \(a\) and \(b\) doesn't matter! Take a moment to convince yourself that \(aba^{2}b=a^{3}b^{2}\) and \(a^{-1}b^{-1}=b^{-1}a^{-1}\). These are not especially deep consequences, but it's useful to be able to do this kind of computation.
Now what do group presentations have to do with symmetry? Let's think about the presentation \(\langle a:a^{3}\rangle\) and rotating a triangle. If our one-third of a full rotation of a triangle is denoted \(a\), rotating by \(a\) three times does nothing: we're back to where we started. Likewise, from the presentation \(\langle a:a^{3}\rangle\) alone, we can conclude facts like \(a^{2}=a^{-1}\): rotating the triangle by \(a\) twice (say counterclockwise twice) is the same as rotating by \(a^{-1}\) once (that is, clockwise once). Take your triangle cutout or look up to the rotations in the Cayley Graph and try it! With the appropriate presentation, all of the geometric information about symmetries is encoded algebraically in the generators and relators. The inverse is also an important strategy: it's fairly typical to run into a presentation without some geometric reference. Figuring out a good geometric analogue to the presentation is one of the best strategies to figuring out information about the symmetries the presentation describes.
Presenting the Symmetries of a Triangle
Our basic problem at this point is to translate back and forth between presentations and our symmetries. Unfortunately, in some technical sense, this is impossible, at least in general. More specifically, the Novikov-Boone tells us, for an arbitrary presentation \(\langle X:R\rangle\), there is no single algorithm that can decide whether a particular word is trivial, can be entirely deleted to get the empty word. (Which is not to say there aren't many, many cases where there is an algorithm that works, just that the general problem is undecidable. This is, in some moral sense, the Halting Problem played out in a different context.)
Still, giving a presentation for the symmetries of a triangle is pretty doable. We have a finite set of positions, so it's possible to just sort of...list everything and call that good. Here's how.
First, we have six positions, so we need six generators. I'm going to somewhat conflate our operations \(r\) and \(f\) with the positions we can reach. You should convince yourself that, starting at triangle 1, \[r, r^{2}, r^{3}, f, fr, fr^{2}\] is a full list of the six positions. Since those are our generators, we can write words like \[(r^{2})(fr)(r^{3})(f)(f)\] and so on. This is already a very messy approach, but we still need our relators, so onward we go!
To get our list of relators, we're going to write the product of each pair of generators and in each order. For example, say we take the product \((r^{2})(fr)\). Since we have listed all six positions, this product ought to be something in our list \(\{r, r^{2}, r^{3}, f, fr, fr^{2}\}\). Going back to the Cayley Graph above and following the path \((r^{2})(fr)\), we find that it is the same as \(fr^{2}\) on our list, so we add the relation \[(r^{2})(fr)=fr^{2}.\] And now we have to do this for every single pair! \[ \begin{array}{c|cccccc} &r &r^{2} &r^{3} &f &fr &fr^{2}\\ \hline r &r^{2} &r^{3} &r &fr^{2} &f &fr\\ r^{2} &r^{3} &r &r^{2} &fr &fr^{2} &f\\ r^{3} &r &r^{2} &r^{3} &f &fr &fr^{2}\\ f &fr &fr^{2} &f &r^{3} &r &r^{2}\\ fr &fr^{2} &f &fr &r^{2} &r^{3} &r\\ fr^{2} &f &fr &fr^{2} &r &r^{2} &r^{3} \end{array} \] If you've taken group theory, you might recognize this as the Cayley Table. In any case, we've list every position, and got six generators and listed every product, and got 36 relators. It works but this is an awful state of affairs! (And if you were my student in a group theory class, I'd still say this isn't actually enough to prove to me you actually have a working presentation, but we're being loosey-goosey.)
So, writing out all the products isn't a great way to go. We can pretty easily do better. As we saw when we were introducing presentations, our multiplicative notation handles a lot of the products. We don't need a relator telling us that the product of \(r\) with itself is \(r^{2}\), that's built in! And actually, just knowing how rotations work handles a lot more. For example, from the relator \(r^{3}=1\), we can conclude \((r^{2})(r^{2})=r^{4}=(r^{3})(r)=r\).
If we take what we know about rotations, namely that \(r^{3}=1\), and flips, namely that \(f^{2}=1\), is that enough for a presentation? Specifically, does the presentation \(\langle r, f : r^{3}, f^{2}\rangle\) describe the symmetries of a triangle? As it turns out, it does not! I'll have to gloss over technical details, but say that it describes a rather more complicated set of symmetries. Here's a 3D view of (part of) the Cayley Graph for those symmetries (you can play around with this yourself in the group presentation visualizer! You'll need to write the relator \(r^{3}\) as \(rrr\) and so on.):
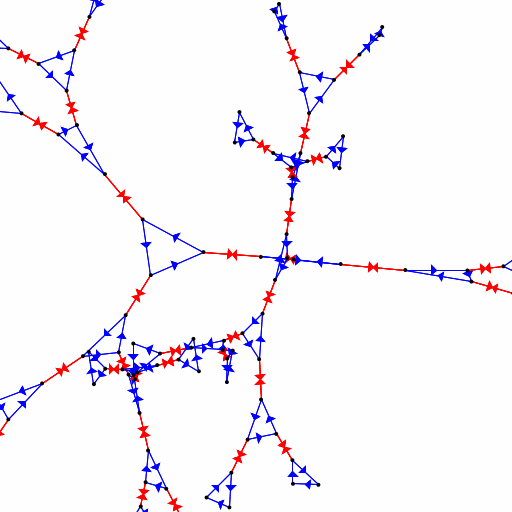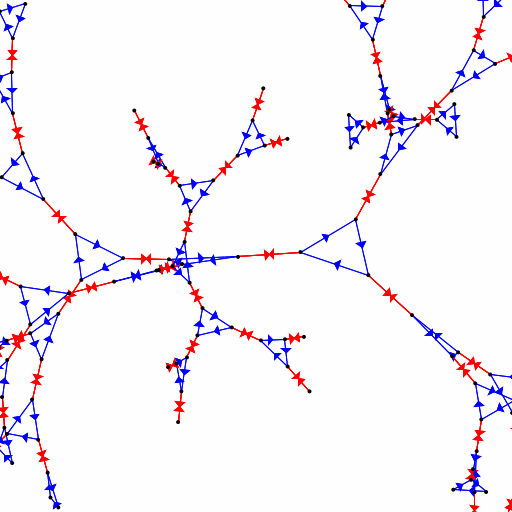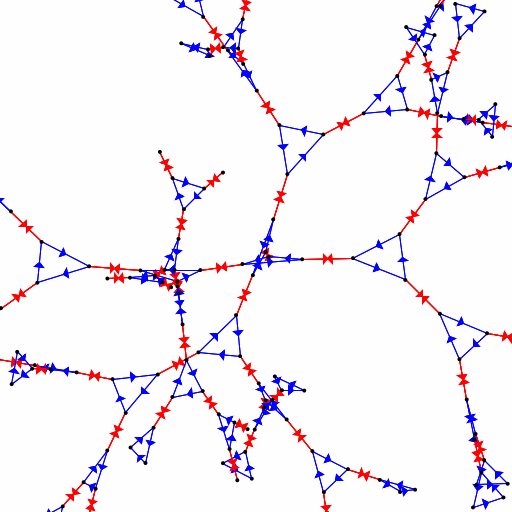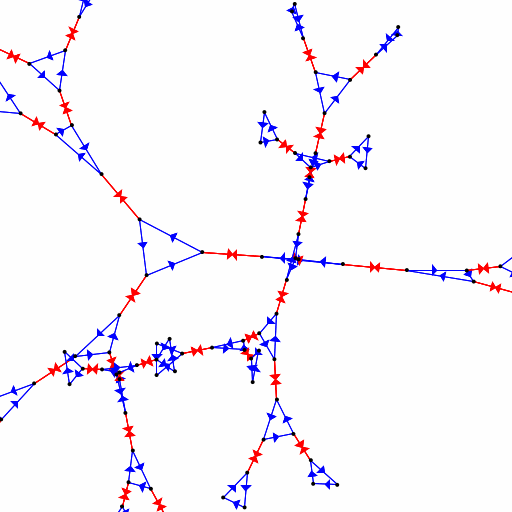 That graphic does suggest something of why our presentation fails: the blue edges correspond to \(r\) and, indeed, those make triangular loops. Likewise, the red edges correspond to \(f\) and they backtrack on themselves, so \(f^{2}=1\). But our presentation doesn't place any restrictions on the product \(rf\) (or \(fr\)) and that causes problems. This is perhaps not too much of a shock: our relators never actually involve a product of both \(r\) and \(f\) so we probably shouldn't expect much to happen on that front. As it turns out, the presentation we want (or, at least, a presentation that works) is \(\langle r, f : r^{3}, f^{2}, (fr)^{2}\rangle\). Using the group presentation visualizer to render this presentation we get:
That graphic does suggest something of why our presentation fails: the blue edges correspond to \(r\) and, indeed, those make triangular loops. Likewise, the red edges correspond to \(f\) and they backtrack on themselves, so \(f^{2}=1\). But our presentation doesn't place any restrictions on the product \(rf\) (or \(fr\)) and that causes problems. This is perhaps not too much of a shock: our relators never actually involve a product of both \(r\) and \(f\) so we probably shouldn't expect much to happen on that front. As it turns out, the presentation we want (or, at least, a presentation that works) is \(\langle r, f : r^{3}, f^{2}, (fr)^{2}\rangle\). Using the group presentation visualizer to render this presentation we get:
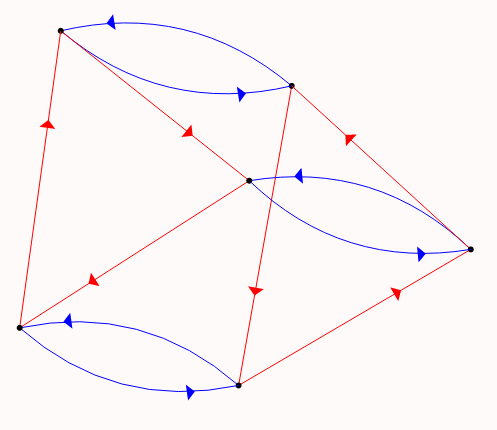 This image of our symmetries shows off something pretty striking: the visualizer is producing the same image as the Cayley Graph above (albeit in 3D, rather than squashed flat)! We're now translating between a geometric representation (the literal symmetries of the paper triangle cutout), to a combinatorial/algebraic representation (the presentation), and back to a different geometric representation (the Cayley Graph).
This image of our symmetries shows off something pretty striking: the visualizer is producing the same image as the Cayley Graph above (albeit in 3D, rather than squashed flat)! We're now translating between a geometric representation (the literal symmetries of the paper triangle cutout), to a combinatorial/algebraic representation (the presentation), and back to a different geometric representation (the Cayley Graph).
Efficiency and Other Presentations
All of the pieces of a sort of word game are in place; as a quick check for yourself, try and come up with the presentation for the symmetries of a square (cut out of paper, just like the triangle). Think about what will have changed from the triangle to a square. Think about what the Cayley Graph would look like. Try plotting your presentation in the visualizer. When you're ready, mouse over to get a possible presentation: \(\langle r, f : r^{4}, f^{2}, (fr)^{2}\rangle\). In general, you can increase the power on \(r\) to match the number of sides for any regular polygon.
We can keep playing this game, but I fear we're starting to land more in stamp collecting than asking interesting mathematical questions about either symmetries or presentations. There are certainly interesting questions to ask with what we've done so far, but I want to hone in on working a particular example pertaining to a classic Group (Co)homology result. You won't need to know anything about cohomology for this; in fact even most mathematicians who know cohomology probably wouldn't have seen this computation anyway. It is, nevertheless, a very accessible result.
For starters, pull up the visualizer and plot the presentation \(\langle a, b : aa, BBaba\rangle\) (the visualizer uses the convention that capital letters are inverses and repeated letters are powers; in our previous discussion of groups presentations, this would be \(\langle a, b : a^{2}, b^{-2}aba\rangle\)). You should notice this is the same as the symmetries of a triangle! Try and work through that fact algebraically, it's a bit subtle. Hint: you can use the relators to conclude \(b^{3}\) is trivial, which is most of the work done.
It turns out, the presentation we came up with for the symmetries of a triangle is actually still redundant! There is a presentation with only two relators, instead of three. (You might ask if we could ever do any better; as it turns out, no. The symmetries of a triangle needs at least two generators and at least two relators. If you ever have fewer relators than generators, you are guaranteed to end up with infinitely many symmetries. Try it in the visualizer, but keep in mind it has a max number of vertices it can display.)
In fact, if you have any regular polygon with an odd number (\(2n+1\)) sides, you can come up with a presentation with two generators and two relators: \(\langle a, b: a^{2}, b^{-(n+1)}ab^{n}a\rangle\). This is something of a special case and is referred to as an efficient presentation. There's lots of interesting things going on with efficient presentations, but here is a curious fact: if you have a regular polygon with an even number of sides (like a square), it does not have an efficient presentation. This is our first fact about group presentations that I would say is genuinely mysterious!
Efficiency and Sphericity
So, why do polygons with an odd number of sides have efficient presentations while polygons with an even number of sides do not? Well, something of a handwaving justification is that an even number of sides is "too symmetric," somehow. That is, when there is an odd number of sides, it's a little less symmetric and we can get away with fewer relators. That is still pretty vague, though, and pinning down an actually usable such notion is tricky. Trying to do so will lead us wandering down notions of group (co)homology and asphericity, which I won't try to do here. Still, I'll show the simple core of a calculation we can do here.
First, we're going to return to the presentation \(\langle r, f : r^{3}, f^{2}, (fr)^{2}\rangle\) and introduce the boundary map. I'm not going to say where this is coming from quite yet, but it's going to turn our presentation into a system of equations. This system of equations will have one variable for each relator and one equation for each generator.
In order, let's say the variables are \(x, y, z\) corresponding to the relators \(r^{3}, f^{2}, (fr)^{2}\). Our equations corresponding to the generators \(r, f\) will be made by summing up the number of occurrences of that generator in a given relator, times the appropriate variable, and set equal to 0. This is a little bit easier to parse as an example:
\[ \begin{cases} 3x+0y+2z=0\\ 0x+2y+2z=0 \end{cases} \]Notice, the first equation corresponds to \(r\). In the relators \(r^{3}, f^{2}, (fr)^{2} \leftrightarrow x, y, z\), we have 3, 0, 2 occurrences of \(r\). The second equation correspond to \(f\) and we have 0, 2, 2 occurrences. The boundary map goes to the Cayley Graph, looks for a polygonal face corresponding to a relator, and reads the number of times a generator occurs as you go around the boundary of that face. You could read in the opposite direction an arrow is pointed, which would negate things; \(-3x-0y-2z=0\) would work just as well for that first equation.
Now, solving this system of equations consists of finding numeric values for \(x, y, z\) that we can plug in to both equations at once and have them all tally to 0. I won't go over this process; if you remember how to solve a system, you should do it! Otherwise, let me just mention that, heuristically, if you ever have more variables than equations you should expect to have lots and lots of possible solutions. In any case, the smallest integer solution to this system is \(x=2,y=3,z=-3\).
Alright, we've made a system of equations using the relators, hinted that there's some geometric meaning with boundaries on the Cayley Graph, but just what exactly is that meaning? And especially what does it mean that there were negative values in the solution I gave?
Let's take a moment to look at the polygonal faces corresponding to the relators.
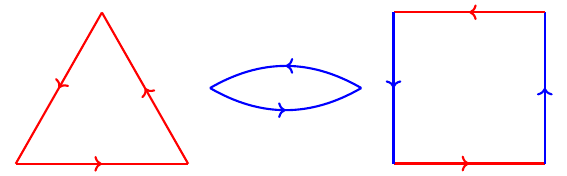
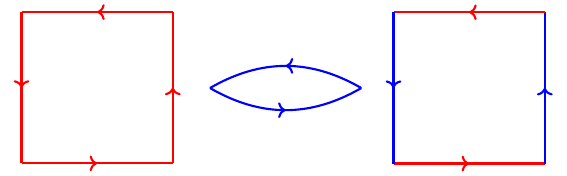
Corresponding to \(r^{3}\) we have a triangle, corresponding to \(f^{2}\) we have a two-gon, and corresponding to \((fr)^{2}\) we have a square. The sides are also colored corresponding to the generators, red for \(r\) and blue for \(f\). They are also oriented; the arrows say to read counterclockwise around each polygon.
Now, the solution to the system of equations was \(x=2,y=3,z=-3\), with \(x\leftrightarrow r^{3}\) (hence corresponding to the triangle), \(y\leftrightarrow f^{2}\) (the two-gon), and \(z\leftrightarrow (fr)^{2}\) (the square). These values are giving us instructions on building some shape out of our three polygons. We'll need two triangles, three two-gons, and -3 squares. We can't really have a negative quantity of squares, but what we can have is squares with their orientation reversed.
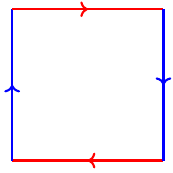
Altogether, that gives us the following eight faces:
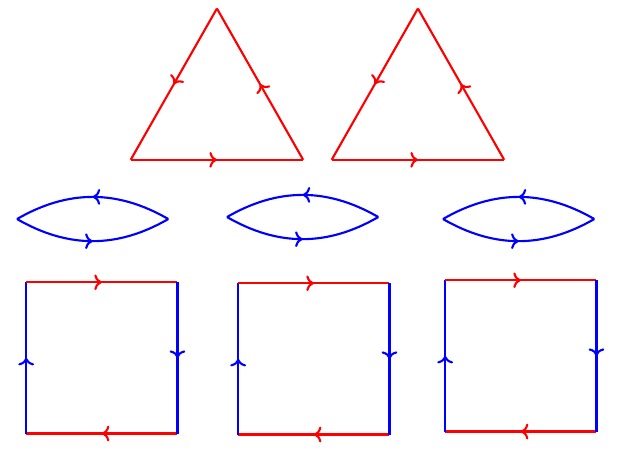
If you've been looking carefully at the pictures so far, you may already know where this is going, but try and match up all the sides of these 8 polygons with a matching color and orientation.
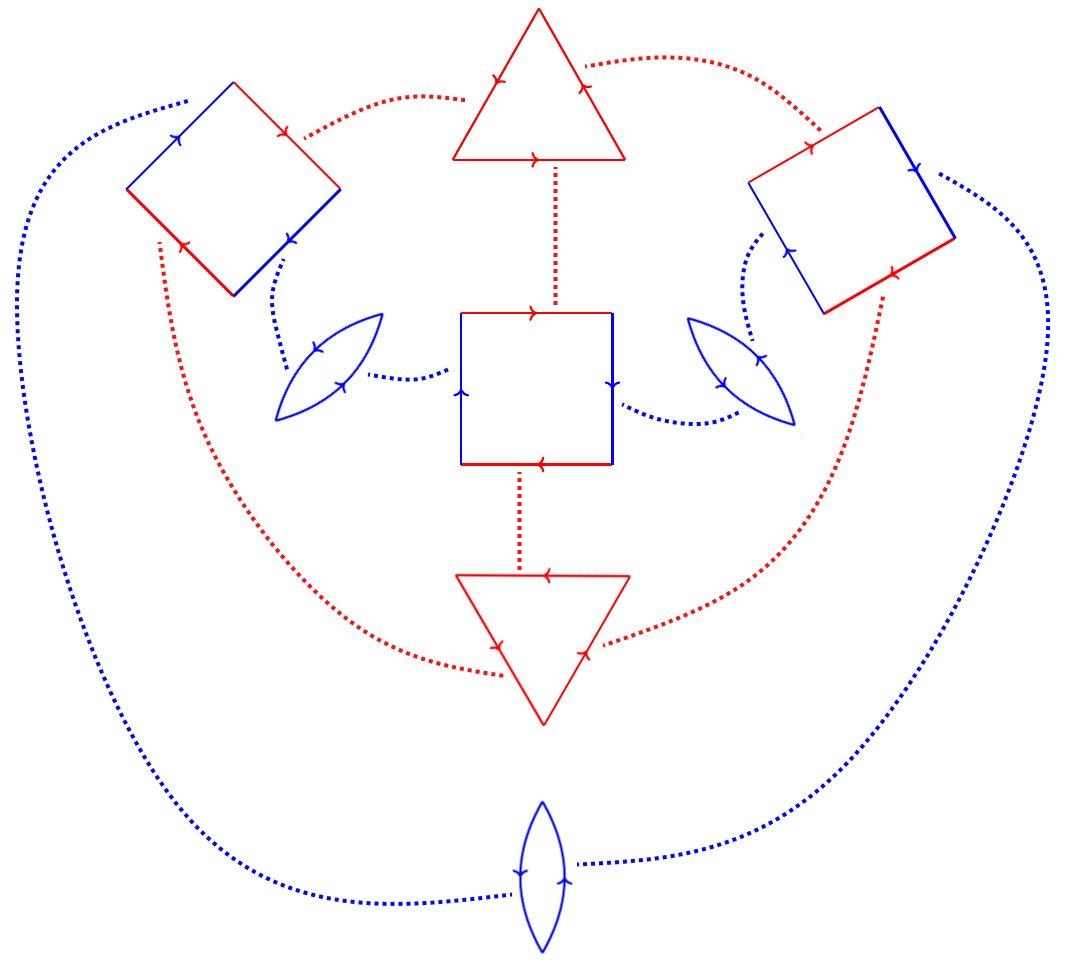
If you cut out all of the faces and glue them together along the matched sides, you get back exactly the Cayley Graph from before, just squashed flat! The solution to that system of equations we got from the boundary map is giving us instructions on what pieces we need to rebuild the particular spherical polyhedron that makes up the Cayley Graph.
Now, we're going to play this same game a second time, but use a presentation for the symmetries of a square, specifically \(\langle r, f : r^{4}, f^{2}, (fr)^{2}\rangle\). If you can, try writing out the system of equations the boundary map gives us in this case, solve it, and assemble pieces like before. After you've tried, read on!
The boundary map gives the following system of equations:
\[ \begin{cases} 4x+0y+2z=0\\ 0x+2y+2z=0 \end{cases} \]It's not very different from the triangular case. The minimal solution is \(x=1,y=2,z=-2\) and it's a little interesting that we have smaller numbers overall in the solution. Most of the process proceeds as before, the only difference is the variable \(x\) which corresponds to the relator \(r^{4}\) gives a square, rather than a triangle. We have the following three faces to arrange:
With our signed count of faces, we want to glue together the following collection of five faces:
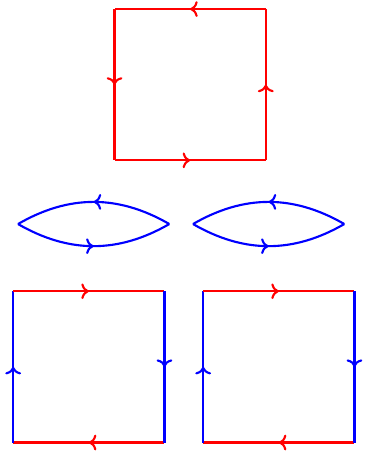
Try to pair up faces as before long enough to convince yourself it's not actually possible. The system of equations we get does not give us instructions on how to reassemble a spherical polyhedron and it's actually that failure in the case of any one presentation that we like that it can never be possible in any presentation to have an equal number of generators and relators.
The Math, in Very Brief
At this point, we somewhat reach the limit of what is doable without more mathematical background. For those of you wanting the specifics, let me run through the argument in brief.
First, it is a classical fact about group (co)homology that, for a finite group, the deficiency (difference in the number of generators and relators) must be at least as big as the number of generators of the second homology (or Schur Multiplier) of the group. This is a nice little argument and I might write it up and link it here at some point in the future. Otherwise, I believe you can find a reference to that fact in D.L. Johnson and E.F. Robertson "Finite groups of deficiency zero" in Homological Group Theory (ed. C.T.C. Wall), C.U.P., 1979.
For that, we need to know how to compute the second homology of a group. To get that, we need a partial resolution of the group. I think of this topologically, so what I need is a topological model of said resolution, up to dimension 3.
Starting from a presentation (actually a presentation two-complex), we can get our partial resolution by killing the second homotopy group via attaching 3-cells (gluing in solid balls anywhere there's a hollow sphere). The second homology of this topological space is then the second homology of our group (as the space provides our partial resolution).
We compute the homology in the routine way: kernel of the boundary map at dimension two (exactly the boundary map in our system of equations before) modulo the image of the boundary map at dimension three. The image of the boundary map is the Hurewicz map applied to the spheres we killed by attaching 3-cells. We see that the minimal solution to our system of equations in the case of the triangle could be assembled into a spherical polyhedron, which we killed (and so the second homology is trivial, and so it's conceivably possible to have a balanced presentation), whereas in the case of the square, we have a solution that is not a spherical polyhedron, and so there must be something in the second homology (and so we must have some deficiency, ie, more relators than generators).
I'll finish with one brief comment: this took a lot of machinery to state a fairly brief result. It'd be reasonable to ask if there's an easier way. For the specific case here (which is secretly even versus odd-ordered dihedral groups), you can probably make an argument that does not invoke all of this machinery explicitly and instead be a little crafty talking about the abelianization of even versus odd-ordered dihedral groups and argue about what possible relators you must have from there. That is mostly just hiding the homological argument, though. In general, it's extremely difficult to bound the deficiency of a group with anything other than homological arguments.