Build a Computer!
I've had, for a little while, vague plans to develop some sort of "play along with Nand2Tetris" game. Since I've also had a fair amount of downtime the past few weeks, I've got a rough implementation of the first 6 chapters, which I think is enough for me to stop. Feel free to jump straight into the application while reading the Nand2Tetris website, or continue reading below to have my very brief introduction.
When you boot into the Build A Computer page, you'll be greeted with the following page:

I've left my various debug tools in place in case anybody wants to jump to a specific portion, so, as it stands, you can unlock everything in the game by default. Otherwise, just hit Start!
Once you've started, you'll be presented with only a few levels to start: AND, NOT, and the CPU Emulator. The CPU Emulator is a simulation of the computer one "builds" in Nand2Tetris, so you can ignore it for now. That leaves AND and NOT. The goal through these initial levels is to study the functional completeness of NAND gates, the idea being that you can start with the logical operation NAND, built from transistors, to build all other logical operators. Opening the AND level, for example, will greet you with a breadboard, two inputs pins, and one output pin. You'll also only have access to NAND gates to add. You can add gates using the menu. Once added, you can click and drag the gates. You can also click and drag between pins to connect them. Right clicking will delete both gates and connections.
Let's work the solution for the AND level as an example. A NAND gate gives the following binary function:
| A | B | A NAND B |
| True (1) | True (1) | False (0) |
| True (1) | False (0) | True (1) |
| True (1) | False (0) | True (1) |
| False (0) | False (0) | True (1) |
Given two inputs, A and B, the output A NAND B is true (or 1) as long as A and B are not BOTH true. Otherwise, the output is false (0). On the simulated breadboard, add two NAND gates and position them how you like. For one of the NAND gates, connect one of each of the breadboard inputs pins to one of each of the NAND gate's input pins. Then, connect the output pin for that NAND gate to BOTH of the input pins for the other NAND gate. Finally, connect that NAND gate's output to the breadboard output. Your board should like the following:
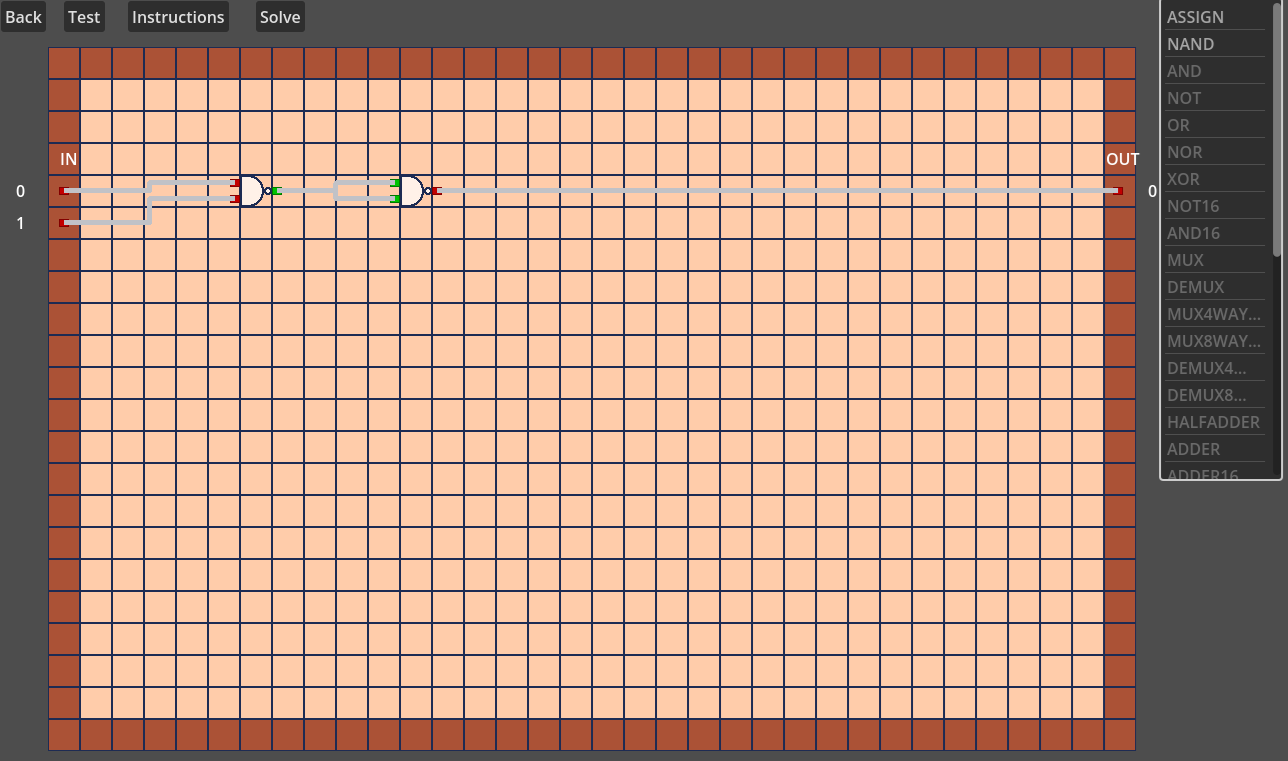
At this point, you can run a test to see that you've wired things up correctly. If all goes well, the breadboard will simulate all possible inputs, the pins switching to red when they are false and green when they are true, and you'll get an alert saying you've solved the level and adding the AND gate to the list of gates you can use.
Each level has a (very sparse) piece of instructions on what output your are trying to produce for a given input. Solving the level unlocks new gates, which make further levels easier, since you have access to more gates. Solving AND and NOT unlocks several more basical logical operator levels (OR, NOR, and XOR). Solving those opens up a broad spread of levels.
The clusters of levels are, roughly, parallel levels (NOT4, AND4, OR4, and OR4WAY) which are, more or less, the same as the previous but with more inputs/outputs, selector levels (MUX and DEMUX) which allow you to select a particular input or to choose a particular output to send an input to, arithmetic primitive levels (HALFADDER and ADDER) which add bits, and memory levels (BIT) which stores and remembers a single bit (true or false). All of these except BIT are "combinatorial," that is, they all "instantly" (barring actual transmission speed of electronics) change the output according to the input.
The BIT level depends on a clocked primitive (the data flip-flop DFF). The DFF is connected to a clock and uses that to maintain its previous output. The BIT takes an input and a load. When a load is applied, the output is set to match the input. When no load is applied, it maintains its previous output. A single MUX chip attached to a DFF, with the DFF also outputting to the MUX creates a BIT.
Solving the various levels in turn results in a couple of major goals. You'll need to make an ADDER8, which is a ripple carry adder, made by chaining together several ADDER gates, which allows for arithmetic. You'll need to make in sequence a REGISTER, RAM8, and RAM64, which allow (recursively) for larger and larger memory (this will unlock RAM16K, the largest memory chip). And you'll need to make the ALU, the arithmetic logic unit, which does all of the computation, using a combination of the ADDER gate, negation gates, AND gates, and several selectors to determine behavior. See chapter 2 of Nand2Tetris for the ALU and chapter 3 for the memory. I include the ALU's instruction table below; this is exactly as given in Nand2Tetris.
| zx (zero input x) | nx (boolean negate input x) | zy (zero input y) | ny (boolean negate input x) | f (if f, out=x+y, else out=x&y) | no (if no, boolean negate out) | out |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | -1 |
| 0 | 0 | 1 | 1 | 0 | 0 | x |
| 1 | 1 | 0 | 0 | 0 | 0 | y |
| 0 | 0 | 1 | 1 | 0 | 1 | !x |
| 1 | 1 | 0 | 0 | 0 | 1 | !y |
| 0 | 1 | 1 | 1 | 1 | 1 | x+1 |
| 1 | 1 | 0 | 1 | 1 | 1 | y+1 |
| 0 | 0 | 1 | 1 | 1 | 0 | x-1 |
| 1 | 1 | 0 | 0 | 1 | 0 | y-1 |
| 0 | 0 | 0 | 0 | 1 | 0 | x+y |
| 0 | 1 | 0 | 0 | 1 | 1 | x-y |
| 0 | 0 | 0 | 1 | 1 | 1 | y-x |
| 0 | 0 | 0 | 0 | 0 | 0 | x&y |
| 0 | 1 | 0 | 1 | 0 | 1 | x|y |
The piece that is not implemented is actually hooking together all the pieces to build a CPU. All the pieces are available to do so, but the level itself does not actually test anything. You'll have to read the architecture chapter (chapter 5) of Nand2Tetris on your own!
With that said, there is a CPU emulator for you to try out. It implements a fragment of the HACK language, described in Nand2Tetris (specifically, the implementation omits variable named lines and no portion of a command may be omitted), a memory-mapped screen (though smaller in size than the screen in Nand2Tetris), and keyboard input. You should read through the appropriate Nand2Tetris chapters if you want more detail.
As a piece of demo Hack assembly code, here's a snippet the fills the screen in black (be careful not to copy+paste a blank line at the end otherwise the code won't assemble):
@16384
D=A-1;null
D=D+1;null
A=D;null
M=-1;null
@16511
null=D-A;JEQ
@2
null=0;JMP